Huy Nguyen
Trứng gà
Đầu tiên xin cảm ơn luận văn của anh Vũ Huy Hợp K15 (C14) đã giúp mình rất nhiều trong việc nghiên cứu động học của Robot Scara
Mình xin tự giới thiệu mình là Huy K19 (C20)
_ Bước đầu tiên của việc nghiên cứu Robot đương nhiên là phải có mô hình rồi nhỉ ? Mình không lo việc đó vì đã có sẵn tay máy của anh Hợp nên mọi chuyện nghe có vẻ thật dễ dàng (dễ thật mà ). Còn nếu bạn không may mắn như mình thì việc đi in 3D có lẽ là cách khả thi nhất nhỉ( thật ra khả thi hơn là bạn ra tiệm mua 1 con đi tầm hơn 3 củ thôi
). Còn nếu bạn không may mắn như mình thì việc đi in 3D có lẽ là cách khả thi nhất nhỉ( thật ra khả thi hơn là bạn ra tiệm mua 1 con đi tầm hơn 3 củ thôi  ).
).
Dưới đây là link các chi tiết 3D các bạn có thể tải về rồi ra tiệm đặt in hoặc dùng máy của lab ha.
https://www.thingiverse.com/thing:1241491
Liên quan đến robot thì có quá nhiều thứ liên quan như động học thuận nghịch rồi điều khiển vận tốc....Hiện tại mình cũng chỉ mới dừng lại ở việc nghiên cứu động học thuận và nghịch thôi . Trong tương lai (không biết khi nào có khi không có luôn
. Trong tương lai (không biết khi nào có khi không có luôn  ) mình sẽ cố gắng tìm hiểu tiếp những phần còn lại nha.
) mình sẽ cố gắng tìm hiểu tiếp những phần còn lại nha.
_ Trước tiên chúng ta thử hình dung 1 chút trong thực tế nhé. Cách tay robot muốn chạm tới 1 vật trong không gian thì phải làm sao nhỉ ? Cách giải quyết là ta chọn 1 hệ trục tọa độ cố định để có tọa độ vật đó nhưng vấn đề khác là robot là một chuỗi các khâu và các khớp nối tiếp. Các khớp này có thể là khớp trượt (tịnh tiến) hay khớp trụ (quay), và chúng có thể sắp xếp theo bất kỳ thứ tự nào và có thể nằm trong bất kỳ mặt phẳng nào. Các khâu cũng có chiều dài bất kỳ kể cả bằng 0, có thể xoắn hoặc cong. Vì vậy bất kỳ một tập hợp các khâu, các khớp đều có thể tạo thành cấu hình một robot. Từ đó việc mô hình hóa phảiđược thực hiện bằng gắn một hệ trục tham chiếu và xác định sự chuyển vị tới khớp tiếp theo. Tổng hợp tất cả ta được một ma trận chuyển vị tổng quát và ma trận D-H sẽ giải quyết vấn đề đó.
Các bạn có thể tham khảo youtube về ma trận Denavit-Hartenberg (D-H) nha. Đây là 1 trong những video bạn có thể tham khảo:
Hoặc xem video chán quá bạn có thể tham khảo slide của môn Kĩ thuật Robot nha
Sau khi hiểu hết tài liệu thì chắc các bạn đã nắm hết lí thuyết phải không vậy cùng mình giải bài toán động học thuận của cánh tay máy phía trên nha.
vậy cùng mình giải bài toán động học thuận của cánh tay máy phía trên nha.
Cấu tạo robot này là 2 khớp quay và 1 khớp tịnh tiến( đại diện cho trục z ) nhưng theo mình thấy 2 khớp quay quan trọng hơn vì nó liên quan đến x và y (thật ra là mình lười làm trục z đó )
)
Bước đầu tiên chúng ta sẽ đặt hệ trục
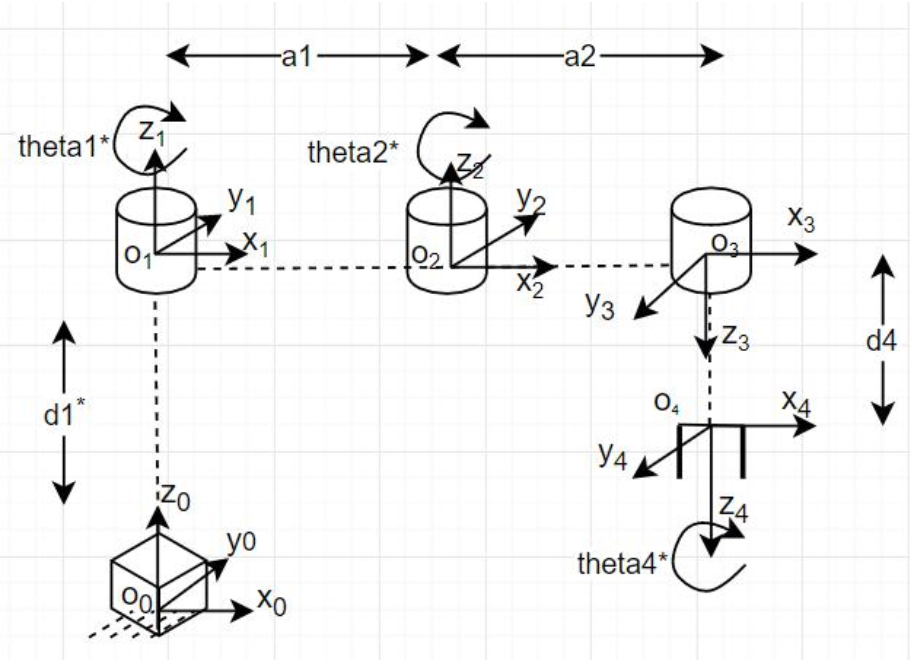
Ở đây ta chỉ cần quan tâm 2 khớp quay theta1 và theta2, dựa theo kiến thức về ma trân D-H và sự hỗ trợ của matlab ta tính được ma trận chuyển vị như sau:
Kết quả thu được là:

Suy ra được ma trận chuyển vị là [ cos(t1 + t2), sin(t1 + t2), 0]
[ sin(t1 + t2), -cos(t1 + t2), 0]
[ 0, 0, -1]
và x=10.7*cos(t1 + t2)+10*cos(t1)
y=10.7*sin(t1 + t2)+10*sin(t1)
Có x và y rồi thì mình sẽ làm việc tiếp theo là vẽ không gian làm việc của tay máy và đây là kết quả:
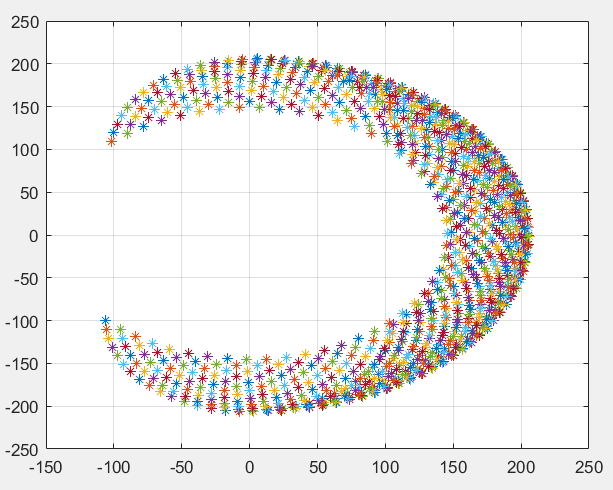
như vậy bài toán động học thuận đã giải quyết xong, đến đây mình xin tạm dừng vì bài viết khá là dài rồi (thật ra mình làm biếng thôi ). Mình sẽ cố gắng update phần động học nghịch và lập trình vđk sau nha. Do nghỉ dịch khá rảnh nên mình sẽ xong sớm thôi. Nếu thấy bài viết hữu ích hãy thả tim cho mình nha
). Mình sẽ cố gắng update phần động học nghịch và lập trình vđk sau nha. Do nghỉ dịch khá rảnh nên mình sẽ xong sớm thôi. Nếu thấy bài viết hữu ích hãy thả tim cho mình nha
Mình xin tự giới thiệu mình là Huy K19 (C20)
_ Bước đầu tiên của việc nghiên cứu Robot đương nhiên là phải có mô hình rồi nhỉ ? Mình không lo việc đó vì đã có sẵn tay máy của anh Hợp nên mọi chuyện nghe có vẻ thật dễ dàng (dễ thật mà
 ). Còn nếu bạn không may mắn như mình thì việc đi in 3D có lẽ là cách khả thi nhất nhỉ( thật ra khả thi hơn là bạn ra tiệm mua 1 con đi tầm hơn 3 củ thôi
). Còn nếu bạn không may mắn như mình thì việc đi in 3D có lẽ là cách khả thi nhất nhỉ( thật ra khả thi hơn là bạn ra tiệm mua 1 con đi tầm hơn 3 củ thôi  ).
).Dưới đây là link các chi tiết 3D các bạn có thể tải về rồi ra tiệm đặt in hoặc dùng máy của lab ha.
https://www.thingiverse.com/thing:1241491
Liên quan đến robot thì có quá nhiều thứ liên quan như động học thuận nghịch rồi điều khiển vận tốc....Hiện tại mình cũng chỉ mới dừng lại ở việc nghiên cứu động học thuận và nghịch thôi
 . Trong tương lai (không biết khi nào có khi không có luôn
. Trong tương lai (không biết khi nào có khi không có luôn  ) mình sẽ cố gắng tìm hiểu tiếp những phần còn lại nha.
) mình sẽ cố gắng tìm hiểu tiếp những phần còn lại nha._ Trước tiên chúng ta thử hình dung 1 chút trong thực tế nhé. Cách tay robot muốn chạm tới 1 vật trong không gian thì phải làm sao nhỉ ? Cách giải quyết là ta chọn 1 hệ trục tọa độ cố định để có tọa độ vật đó nhưng vấn đề khác là robot là một chuỗi các khâu và các khớp nối tiếp. Các khớp này có thể là khớp trượt (tịnh tiến) hay khớp trụ (quay), và chúng có thể sắp xếp theo bất kỳ thứ tự nào và có thể nằm trong bất kỳ mặt phẳng nào. Các khâu cũng có chiều dài bất kỳ kể cả bằng 0, có thể xoắn hoặc cong. Vì vậy bất kỳ một tập hợp các khâu, các khớp đều có thể tạo thành cấu hình một robot. Từ đó việc mô hình hóa phảiđược thực hiện bằng gắn một hệ trục tham chiếu và xác định sự chuyển vị tới khớp tiếp theo. Tổng hợp tất cả ta được một ma trận chuyển vị tổng quát và ma trận D-H sẽ giải quyết vấn đề đó.
Các bạn có thể tham khảo youtube về ma trận Denavit-Hartenberg (D-H) nha. Đây là 1 trong những video bạn có thể tham khảo:
Sau khi hiểu hết tài liệu thì chắc các bạn đã nắm hết lí thuyết phải không
 vậy cùng mình giải bài toán động học thuận của cánh tay máy phía trên nha.
vậy cùng mình giải bài toán động học thuận của cánh tay máy phía trên nha.Cấu tạo robot này là 2 khớp quay và 1 khớp tịnh tiến( đại diện cho trục z ) nhưng theo mình thấy 2 khớp quay quan trọng hơn vì nó liên quan đến x và y (thật ra là mình lười làm trục z đó
 )
)Bước đầu tiên chúng ta sẽ đặt hệ trục
Ở đây ta chỉ cần quan tâm 2 khớp quay theta1 và theta2, dựa theo kiến thức về ma trân D-H và sự hỗ trợ của matlab ta tính được ma trận chuyển vị như sau:
Code:
t=eye(4);
a1=10
a2=10.6
syms t1 t2
a=[cos(t1) -sin(t1) 0 a1*cos(t1);sin(t1) cos(t1) 0 a1*sin(t1);0 0 1 0;0 0 0 1]
b=[cos(t2) sin(t2) 0 a2*cos(t2); sin(t2) -cos(t2) 0 a2*sin(t2);0 0 -1 0;0 0 0 1]
t=a*b
simplify(t)
Code:
t =
[ cos(t1)*cos(t2) - sin(t1)*sin(t2), cos(t1)*sin(t2) + cos(t2)*sin(t1), 0, 10*cos(t1) + (53*cos(t1)*cos(t2))/5 - (53*sin(t1)*sin(t2))/5]
[ cos(t1)*sin(t2) + cos(t2)*sin(t1), sin(t1)*sin(t2) - cos(t1)*cos(t2), 0, 10*sin(t1) + (53*cos(t1)*sin(t2))/5 + (53*cos(t2)*sin(t1))/5]
[ 0, 0, -1, 0]
[ 0, 0, 0, 1]
ans =
[ cos(t1 + t2), sin(t1 + t2), 0, (53*cos(t1 + t2))/5 + 10*cos(t1)]
[ sin(t1 + t2), -cos(t1 + t2), 0, (53*sin(t1 + t2))/5 + 10*sin(t1)]
[ 0, 0, -1, 0]
[ 0, 0, 0, 1][ sin(t1 + t2), -cos(t1 + t2), 0]
[ 0, 0, -1]
và x=10.7*cos(t1 + t2)+10*cos(t1)
y=10.7*sin(t1 + t2)+10*sin(t1)
Có x và y rồi thì mình sẽ làm việc tiếp theo là vẽ không gian làm việc của tay máy và đây là kết quả:
như vậy bài toán động học thuận đã giải quyết xong, đến đây mình xin tạm dừng vì bài viết khá là dài rồi (thật ra mình làm biếng thôi
 ). Mình sẽ cố gắng update phần động học nghịch và lập trình vđk sau nha. Do nghỉ dịch khá rảnh nên mình sẽ xong sớm thôi. Nếu thấy bài viết hữu ích hãy thả tim cho mình nha
). Mình sẽ cố gắng update phần động học nghịch và lập trình vđk sau nha. Do nghỉ dịch khá rảnh nên mình sẽ xong sớm thôi. Nếu thấy bài viết hữu ích hãy thả tim cho mình nha
Last edited:
