0. Phân tích từ vựng "biến ngẫu nhiên":
Khi đó, ta ký hiệu:
\[ \begin{equation} P(X=x) \end{equation} \]
là xác suất biến ngẫu nhiên \(X\) có giá trị là \(x\).
Mỗi lần tung đồng xu, \(X\) đều có thể nhận một trong hai giá trị ngửa hoặc sấp, điều này thể hiện tính ngẫu nhiên. Tuy nhiên nếu số lần tung đồng xu đủ lớn thì sau khi thống kê lại, ta sẽ thấy số lần xuất hiện mặt ngửa \(X = head\) và số lần xuất hiện mặp sấp \(X = tail\) là như nhau:
\[ \begin{equation} P(X=head) = P(X=tail) = \frac{1}{2} \end{equation} \]
Kết luận \(X\) là biến ngẫu nhiên vì ta thấy mỗi lần tung biến \(X\) đạt một giá trị ngẫu nhiên nhưng thống kê lại cuối cùng vẫn tuân theo quy luật xác suất: với số lượng phép thử đủ lớn, số lần xuất hiện mặt ngửa và sấp là như nhau.
2. Ví dụ 2: Cảm biến Lidar-Lite dùng tia laser để đo khoảng cách.
Giá trị khoảng cách đo được khi dùng Lidar-Lite thường được xem là một biến có giá trị ngẫu nhiên nhưng vẫn tuân theo quy luật phân phối chuẩn với trung bình (mean) là \(\mu\) và độ lệch chuẩn (standard deviation) là \( \sigma \). Phương trình của phần phối chuẩn 1 chiều (1 biến) là:
\begin{equation}
\mathcal{N}(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}}
\end{equation}
Với một khoảng cách thực tế không đổi, mỗi một lần đo, cảm biến sẽ trả lại những giá trị khác nhau mà ta xem là ngẫu nhiên. Tuy nhiên khi thống kê lại thì ta thấy các giá trị này vẫn ở gần giá trị trung bình theo phân phối chuẩn.
Thống kê như thế nào: Giả sử tường cách sensor 20cm, xung quanh 20cm đó, ta chia thành một số đoạn (ví dụ như đoạn 16-18, 18-20, 20-22, 22-24). Với mỗi đoạn ta có một biến đếm đếm số lần khoảng cách đo được rồi vào đoạn đó. Ta thực hiện một số lượng lớn phép đo, với mỗi phép đo, nếu khoảng cách đo được thuộc đoạn nào, ta cộng biến đếm của đoạn đó lên 1. Chia biến đếm của mỗi đoạn cho tổng số lần thực hiện phép đo, trong trường hợp lý tưởng ta có đồ thị thống kê tương tự như hình sau:
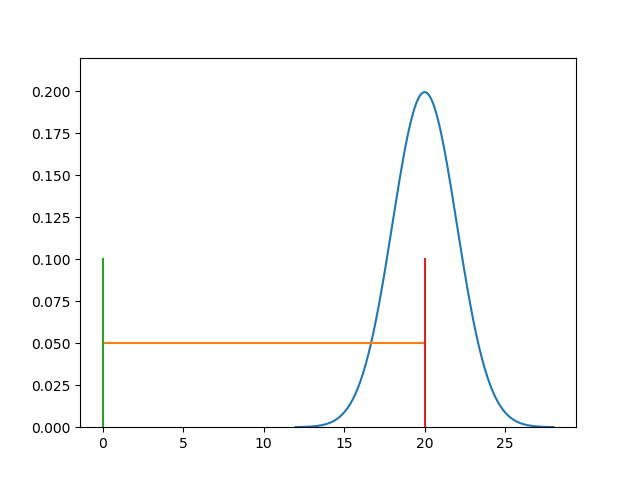
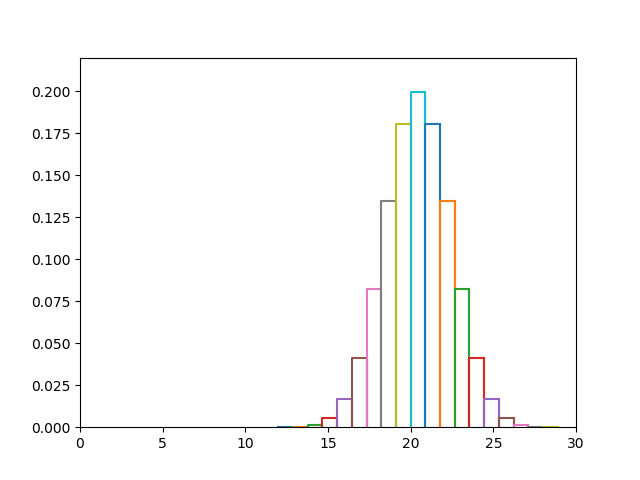Nếu số lượng phép đo đủ nhiều và số lượng khoảng chia đủ lớn (mỗi khoảng chia sẽ nhỏ hơn) thì ta sẽ được một đồ thị liên tục của phân phối chuẩn như hình sau:
Ví dụ 3: Cảm biến RPLIDAR-A1 sử dụng laser để đo khoảng cách.
Mỗi lượt đo, cảm biến sẽ trả lại 360 giá trị là khoảng cách tới 360 điểm xung quanh lidar. Đối với RPLIDAR-A1 sensor, khái niệm biến được mở rộng, biến ngẫu nhiên \(X\) sẽ có 360 chiều, mỗi giá trị \(x\) của \(X\) sẽ là một vector gồm 360 phần tử. Các giá trị của biến ngẫu nhiên \(X\) thường được xem tuân theo quy luật phân phối chuẩn nhiều chiều (multivariate):
\begin{equation}
\mathcal{N}(x | \mu, \Sigma) = \det{(2\pi\Sigma)}^{-\frac{1}{2}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}
\end{equation}
Với:
Một cách lý tưởng, giả sử mỗi lần đo khoảng cách của RPLIDAR-A1 trong một lượt 360 lần đo là độc lập với nhau thì:
\begin{equation}
\Sigma =
\begin{bmatrix}
\sigma_0^2 & 0 & ... & 0 \\
0 & \sigma_1^2 & ... & 0 \\
0 & 0 & ... & \sigma_{359}^2 \\
\end{bmatrix}
\end{equation}
Lý tưởng hơn, giả sử mỗi lần đo khoảng cách của RPLIDAR-A1 trong một lượt 360 lần đo là độc lập với nhau và sai số của mỗi phép đo là như nhau, khi đó:
\begin{equation}
\Sigma =
\begin{bmatrix}
\sigma^2 & 0 & ... & 0 \\
0 & \sigma^2 & ... & 0 \\
0 & 0 & ... & \sigma^2 \\
\end{bmatrix}
\end{equation}
Nhờ việc lý tưởng hóa \(\Sigma\), ta có thể tính được nghịch đảo của \(\Sigma\) (nghịch đảo ma trận chéo hay inverse of diagonal matrix) và nhân nó với hai vector hai bên dễ dàng hơn rất nhiều.
Tổng kết: 3 ví dụ trên cho ta 3 trường hợp của biến ngẫu nhiên theo thứ tự từ đơn giản đến phức tạp:
- Thứ nhất: là biến, giá trị biến có tính chất là có thể thay đổi được, đối lập với hằng (giá trị không thay đổi được);
- Thứ hai: là ngẫu nhiên, tức là giá trị đạt được của biến không bị tác động bởi bất kỳ yếu tố nào. Lý thuyết là không chịu tác động nhưng thực tế thì có thể linh hoạt hơn: chịu tác động nhỏ hoặc chịu tác động của các yếu tố không xét đến.
- Thứ ba: mặc dù ngẫu nhiên nhưng vẫn phải tuân theo quy luật xác xuất nào đó;
Khi đó, ta ký hiệu:
\[ \begin{equation} P(X=x) \end{equation} \]
là xác suất biến ngẫu nhiên \(X\) có giá trị là \(x\).
Mỗi lần tung đồng xu, \(X\) đều có thể nhận một trong hai giá trị ngửa hoặc sấp, điều này thể hiện tính ngẫu nhiên. Tuy nhiên nếu số lần tung đồng xu đủ lớn thì sau khi thống kê lại, ta sẽ thấy số lần xuất hiện mặt ngửa \(X = head\) và số lần xuất hiện mặp sấp \(X = tail\) là như nhau:
\[ \begin{equation} P(X=head) = P(X=tail) = \frac{1}{2} \end{equation} \]
Kết luận \(X\) là biến ngẫu nhiên vì ta thấy mỗi lần tung biến \(X\) đạt một giá trị ngẫu nhiên nhưng thống kê lại cuối cùng vẫn tuân theo quy luật xác suất: với số lượng phép thử đủ lớn, số lần xuất hiện mặt ngửa và sấp là như nhau.
2. Ví dụ 2: Cảm biến Lidar-Lite dùng tia laser để đo khoảng cách.
Giá trị khoảng cách đo được khi dùng Lidar-Lite thường được xem là một biến có giá trị ngẫu nhiên nhưng vẫn tuân theo quy luật phân phối chuẩn với trung bình (mean) là \(\mu\) và độ lệch chuẩn (standard deviation) là \( \sigma \). Phương trình của phần phối chuẩn 1 chiều (1 biến) là:
\begin{equation}
\mathcal{N}(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}}
\end{equation}
Với một khoảng cách thực tế không đổi, mỗi một lần đo, cảm biến sẽ trả lại những giá trị khác nhau mà ta xem là ngẫu nhiên. Tuy nhiên khi thống kê lại thì ta thấy các giá trị này vẫn ở gần giá trị trung bình theo phân phối chuẩn.
Thống kê như thế nào: Giả sử tường cách sensor 20cm, xung quanh 20cm đó, ta chia thành một số đoạn (ví dụ như đoạn 16-18, 18-20, 20-22, 22-24). Với mỗi đoạn ta có một biến đếm đếm số lần khoảng cách đo được rồi vào đoạn đó. Ta thực hiện một số lượng lớn phép đo, với mỗi phép đo, nếu khoảng cách đo được thuộc đoạn nào, ta cộng biến đếm của đoạn đó lên 1. Chia biến đếm của mỗi đoạn cho tổng số lần thực hiện phép đo, trong trường hợp lý tưởng ta có đồ thị thống kê tương tự như hình sau:
Ví dụ 3: Cảm biến RPLIDAR-A1 sử dụng laser để đo khoảng cách.
\begin{equation}
\mathcal{N}(x | \mu, \Sigma) = \det{(2\pi\Sigma)}^{-\frac{1}{2}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}
\end{equation}
Với:
- \( x = (x_0, x_1,... , x_{359}) \) là một giá trị có để đạt được của \(X\);
- \( \mu = (\mu_0, \mu_1,... ,\mu_{359}) \) là trung bình của \(X\);
- \(\Sigma\) là độ lệch hay còn gọi là ma trận hiệp phương sai;
Một cách lý tưởng, giả sử mỗi lần đo khoảng cách của RPLIDAR-A1 trong một lượt 360 lần đo là độc lập với nhau thì:
\begin{equation}
\Sigma =
\begin{bmatrix}
\sigma_0^2 & 0 & ... & 0 \\
0 & \sigma_1^2 & ... & 0 \\
0 & 0 & ... & \sigma_{359}^2 \\
\end{bmatrix}
\end{equation}
Lý tưởng hơn, giả sử mỗi lần đo khoảng cách của RPLIDAR-A1 trong một lượt 360 lần đo là độc lập với nhau và sai số của mỗi phép đo là như nhau, khi đó:
\begin{equation}
\Sigma =
\begin{bmatrix}
\sigma^2 & 0 & ... & 0 \\
0 & \sigma^2 & ... & 0 \\
0 & 0 & ... & \sigma^2 \\
\end{bmatrix}
\end{equation}
Nhờ việc lý tưởng hóa \(\Sigma\), ta có thể tính được nghịch đảo của \(\Sigma\) (nghịch đảo ma trận chéo hay inverse of diagonal matrix) và nhân nó với hai vector hai bên dễ dàng hơn rất nhiều.
Tổng kết: 3 ví dụ trên cho ta 3 trường hợp của biến ngẫu nhiên theo thứ tự từ đơn giản đến phức tạp:
- Ví dụ 1: Biến ngẫu nhiên 1 chiều có giá trị rời rạc (ngửa hoặc sấp);
- Ví dụ 2: Biễn ngẫu nhiên 1 chiều có giá trị liên tục (khoảng cách);
- Ví dụ 3: Biến ngẫu nhiên nhiều chiều (ví dụ này cụ thể là 360 chiều) có giá trị liên tục;